これまでのシミュレーションでは、乱数に メルセンヌ・ツイスターを用いてきた。 メルセンヌ・ツイスターは「従来にない長周期, 高次元均等分布を」持った、性質の良い乱数である。 それでは、反対に、周期が短く不均等な、性質の悪い乱数を用いてシミュレーションを行ったらどうなるだろうか。

シミュレーション８、シミュレーション９では、 連成振動子の列を用いてシミュレーションを行ったが、一方向の流れは確認できなかった。 その理由は、おそらく連成振動子の列が”性質の良い乱数”になっていないからではないか。 であれば、”性質の悪い”乱数を用いたならば一方向の流れが生じない、といった予想が成り立つ。

上の予想を確かめるため、シミュレーション１２で分子数２個のケースを、性質の悪い乱数に置き換えて実施した。 性質の悪い乱数として、線形合同法による次のような乱数列R[n]を用いた。

乱数列と言うより、むしろ周期的な数列に近い。

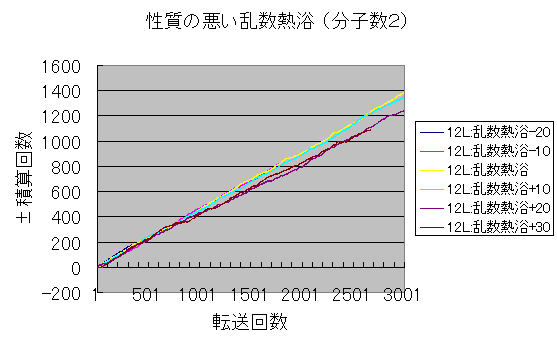
結果は予想に反して、正(＋)の転送が高い頻度で起こっていた。
元のシミュレーション１２と比べると、グラフの揺らぎが少なく、直線的だ。
また、ワープゾーンの位置の偏りの影響が小さい（全てのグラフがほとんど重なっている）。

なぜこのような結果になったのか。 乱数列の周期と、仕掛けの動作周期がたまたま一致した場合には、このように綺麗に直線的な結果が出るのだろうか。 いまのところ良い説明が思い付かない。 １つだけ確かなのは、乱数の善し悪しによって結果が左右される、ということだ。