乱数による熱浴ではなく、力学的な仕組みだけを組み合わせてエネルギーの流れを確認することはできないだろうか。
シミュレーション8,9では、一次元の連成振動子を用いたが、一方向のエネルギーの流れは確認できなかった。
一次元の連成振動子では、性質の良い乱数のように均一な分布を実現するのは困難であろう。
そこで、連成振動子の代わりに、カオス的な運動を行う系を用いてシミュレーションを試みた。
下に示すような系を想定し、いろいろとシミュレーションを試みたのだが、いずれにおいても明確な一方向のエネルギーの流れは確認できなかった。
1.2次元の連成振動子
連成振動子を一次元ではなく、2次元に配置する。
分子は平面上に、3角形の格子状(トラス状)に配置する。
このとき、相互作用が前後1個の分子だけでなく、前後複数個に渡って及ぶようにする。
前のシミュレーション10とは内容的には別の物です。
2.多体問題の応用
互いに引き合う多数の分子を用意し、2つの等温壁の間に置く。
分子同士は引力によって、分子と等温壁は衝突によって、力を伝達する。
3.エノンのカオスを並べる
”エノンのカオス”と呼ばれる、三角形状のポテンシャルの中に分子を置いたものを並べる。
分子間に引力を働かせ、力の伝達を行った。
4.ばね振り子を並べる
ばねの先に質点をぶら下げた振り子を複数個用意し、一列に並べた。
それぞれの質点同士をバネで結んで力の伝達を行った。
なぜ乱数による熱浴であればエネルギーは一方向に流れるのに、力学的なカオスでは一方向の流れが実現できないのだろうか?
ここで、乱数による熱浴シミュレーションとカオスシミュレーションを比較して、ある1つのプロセスの導入を試みた。
それは「エネルギーを等分配する」プロセスである。
等温壁に分子が衝突したとき、分子の持つ運動エネルギーと、等温壁の持つ運動エネルギーの差が小さくなるようにエネルギーを再分配した。
カオスシミュレーションでは、等温壁という1つの振動子と、分子の衝突によって、エネルギーの分配を行っていた。
そこには恣意的に「エネルギーを等分配する」、「平均化する」というプロセスが組み込まれているわけではない。
一方、乱数によるエネルギーの交換では、結果としてエネルギーが平均化されることになる。
この差異に着目し、エネルギーを等分配するプロセスをカオスシミュレーションに組み入れたのである。
ばね振り子を並べた系に、等温壁でエネルギー等分配を行うプロセスを組み込んだシミュレーションを行った。 その結果、はっきりとした一方向のエネルギーの流れが確認できた。
以上より得られる帰結は、 「一方向のエネルギーの流れを作り出すには、”エネルギーを等分配する”プロセスが不可欠」 ということだ。
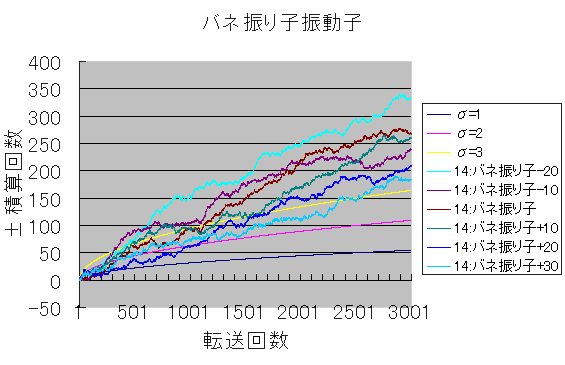
(σ=1、σ=2、σ=3 のグラフは、転送回数が有意かどうかの判断基準として付け加えた補助的な線)
ワープゾーンの偏り無し (上のグラフで"14:バネ振り子" 茶色の線に対応する)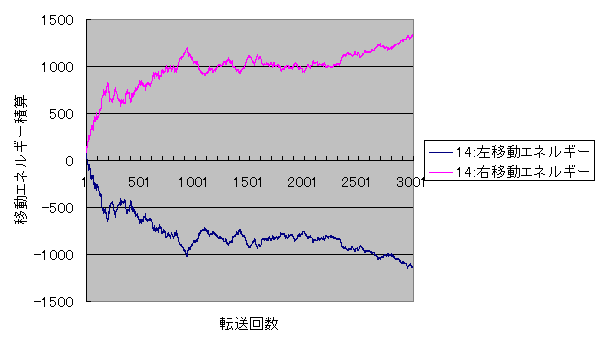
エネルギーが左側から流入し、右側に流出していることがわかる。
開始から1000回目付近までの積算値の変化は、それ以降に比べて急になっている。
これは、初期の状態から定常的な状態に至るまでの緩和過程が含まれているからであろう。
1000回目以降の積算値の変化は緩やかになるが、止まってはいない。



