準備段階その3。 先のシミュレーション1に、中央の隔壁を一瞬で別の位置に移動させる仕掛けを入れる。 この仕掛けのことを「ワープゾーン」と呼ぶことにしよう。 ワープゾーンとは、次のような仕掛けのことだ。
・1つの部分は中央付近に、もう1つの部分は左右どちらかに片側に位置付ける。
それぞれの部分を、ゾーンA、ゾーンBと呼ぶことにしよう。
・2つの部分(ゾーン)の大きさは等しいものとする。
・もし隔壁がゾーンAにあって、2つのボールが2つのゾーンの外側にあれば、隔壁を瞬時にゾーンBに移動する。
・反対に隔壁がゾーンBにあって、2つのボールが2つのゾーンの外側にあれば、隔壁を瞬時にゾーンAに移動する。
(2つのゾーンの外側とは、ボールが (ゾーンA)∪(ゾーンB)∪(ゾーンAとBの間の領域) には無いとき、ということ。 要は、2つのボールが常に隔壁の左右に分かれるようにする、ということだ。)
・一度隔壁が移動した後は、一定時間次の移動は行われない。
そうしないと、隔壁が2つのゾーン間を行ったり来たりすることになるので。
一定時間を経過してもなお、隔壁がゾーンの上に留まっていたら、そのときには次の転送が起こって隔壁は再び元のゾーンに転送される。
・転送前の隔壁の速度と、転送後の隔壁の速度は等しい。
また、ゾーン内での隔壁の相対的な位置は、転送前と転送後で保たれる。
(そのために2つのゾーンの大きさは等しくなっているのだ)
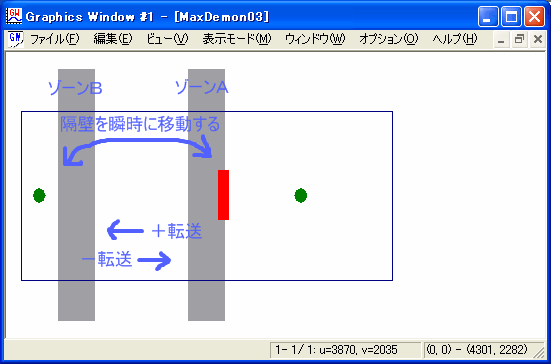
ワープゾーンとは、要するにA ←→ B間を瞬時に移動する「転送装置」のことだ。 (SF映画「スタートレック」に登場する小道具、あるいは「ハエ男の恐怖」のようなものだ。) 言葉による説明より、実際にシミュレーションを見てもらった方が理解が早いだろう。 どうやってワープゾーンを実現するか、という話はひとまず置いておいて、ここでは「仮にこのようなワープゾーンがあったとしたら」という仮定のもとに話を進めることにする。 A→Bへの転送を、ここでは便宜的に正方向(+)の転送、とする。 逆に、B→Aの転送を、ここでは便宜的に負方向(−)の転送、としよう。
さて、ここで問題。 長時間観察したとき、正方向(+)の転送と負方向(−)の転送は、どちらがより多く行われることになるか? もし2つのゾーンが左右対称に配置されていれば、おそらく正負の転送回数は等しくなるだろう。 それでは、左右対称ではなく、どちらか一方の側に片寄せてゾーンを配置したら?
答はシミュレーションを動かしてみれば分かる。 直感に反して(あるいは直感通り、という人もいるかもしれないが)ゾーンを片側に寄せても、正負の転送回数は等しくなる。 ワープゾーンの位置が非対称だからといって、転送回数が正負で非対称になるわけではない。 隔壁の位置の分布をシミュレーション1と比較しても、はっきりとした違いは認められない。 また、左右のボールの速度にも有意な差は認められない。 つまり、ワープゾーンという仕掛けを施す前と後で、何も変わっていないということだ。
さて、ここからが本命だ。 上のシミュレーション3と同じことを、今度は「左右のボールの速度をできるだけ一定に保った状態で」行ってみる。 ボールの速度を一定に保つ方法は、先のシミュレーション2と同様だ。
そして、ここでも先のシミュレーション3と同じ問を発してみる。 時間観察したとき、正方向(+)の転送と負方向(−)の転送は、どちらがより多く行われることになるか?
シミュレーションの結果は、明らかに非対称な傾向を示す。 ゾーンの位置を非対称に、左右どちらか片側に寄せた場合、それに応じて正負の転送は、正または負のどちら一方がより多く起こるようになる。 先のシミュレーション3の結果と比較すれば、違いは一目瞭然だ。
・シミュレーション4: 正負いずれか一方の転送が優位
「えっ!何のこと?」と思っている人、心配ご無用。 何のことか分からないのが当然です。 以下においおい説明しましょう。
グラフは正負の転送についての積算回数を表している。
積算回数が正(+)であれば、それだけ正方向(+)の転送が負方向(−)の転送より多く行われたことになる。
縦軸は正負合わせた転送回数。
各シミュレーションは、転送が1000回行われるまで実施した。
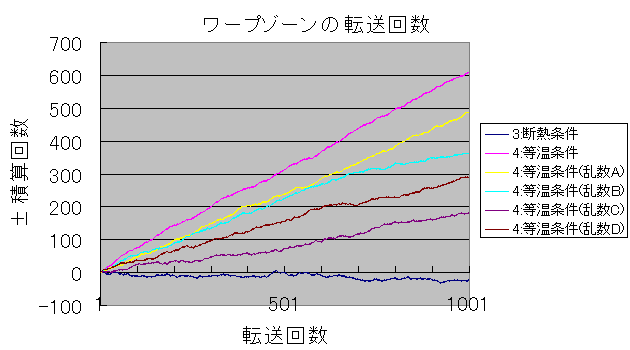
3:断熱条件(シミュレーション3)では、正負の転送回数に明確な差異が見られない。
4:等温条件(シミュレーション4)では、正方向(+)の転送が負方向(−)の転送より明らかに多い。



