まずは準備段階。 とにかく動かしてみよう。 一次元の有限の範囲内を動く、２個のボールの間に１枚の隔壁がある。 ボールは両端と隔壁で反射する。 隔壁はボールに押されて移動する。

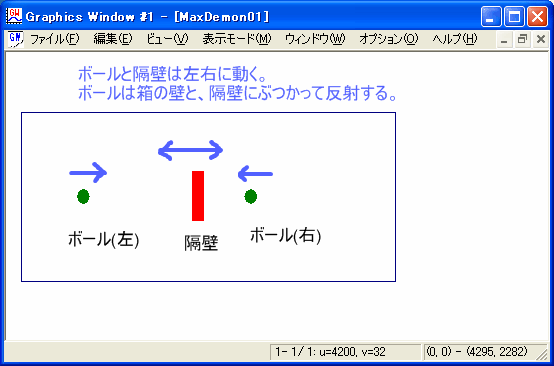
ここで確認しておきたいののは「隔壁の位置」である。 長時間に渡って観察したとき、隔壁の位置はどのような分布を示すだろうか。 直感的にわかることだが、隔壁は平均して中央にある確率が最も高い。 左右対称なのだから、当然といえば当然だろう。

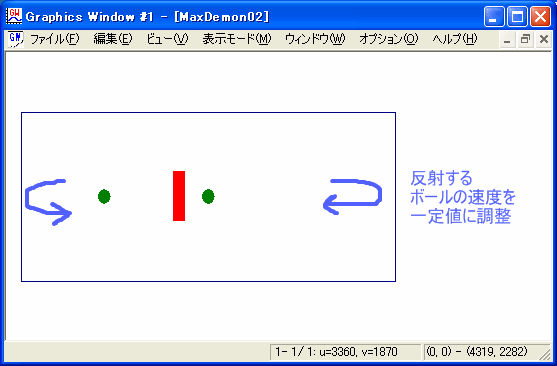
準備段階その２。 シミュレーション１と同じことを、今度は「左右のボールの速度をできるだけ一定に保ったまま」行ってみる。

左右のボールの速度を等しく保つために、右端と左端の反射に細工を施す。 右端と左端でボールが反射するたびに、ボールの反射後の速度を一定の平均値に近づける。 そうなるように、ボールに対して適切に加速・減速を行う。 具体的には

といった操作を行う。
例えば、ボールの反射前の速度が2で、一定の平均速度が1だとしたら、反射後の速度は となる。 何度も反射を繰り返すうちに、ボールの速度は次第に一定の平均速度に近づくことになる。 2 -> 1.5 -> 1.25 -> 1.125 -> 1.0625 -> ... といった具合に。 （実際のシミュレーションでは両端の反射の他に、隔壁との反射もあるので、必ずしもここに並べた数字通りにはならない。）

上ではボールの平均速度を固定した平均速度に近づける操作を行ったが、次に、平均速度にある程度の乱数を加えてばらつきを持たせた状態でシミュレーションを行ってみよう。 乱数の加え方として、次の４パターンについて調べた。

ここでもシミュレーション１と同様、隔壁の位置を調べてみよう。 今度の場合も左右対称なので、やはり隔壁は中央付近に位置する確率が最も高い。

グラフは隔壁の位置を一定間隔で数え上げたものである。
横軸は隔壁の位置を表しており、１が左端、２０が右端、１０が中央付近である。
縦軸はその位置に隔壁があった頻度を表している。
頻度は各シミュレーションごとに３０００回ずつカウントしている。

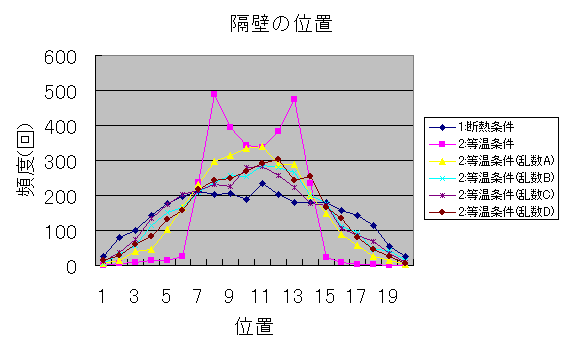
ほとんどのシミュレーションでは、中央付近が最も頻度が高くなっている。
条件の違いによって、分散（裾野の広がり具合）が若干異なっている。
2:等温条件（乱数なしでボールの速度を一定値に近づけたもの）では、最も頻度の高いピークが２つ見られる。 これは、ボールと隔壁の反射が左右交互に一定の周期で行われた結果である。