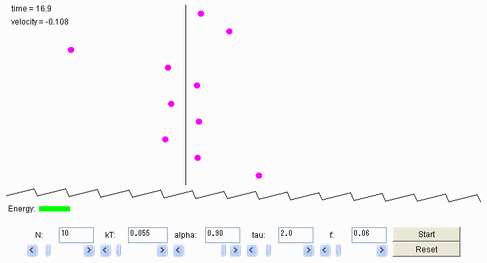
筋肉が熱ゆらぎを利用して運動していることを認めたとすれば、いったいどのような仕組みで動いているのか興味がつのる。

熱ゆらぎを利用するモデルとして、真っ先に思い当たるのがファインマンズ・ラチェットであろう。（第一章 05 を参照） 筋肉の仕組みを熱ゆらぎから説明するモデルは幾つか提案されているが、基本的な発想はファインマンズ・ラチェットをベースにしたものが多いようだ。 もちろんファインマンズ・ラチェットは温度差の全くない環境下で動作することはできない。 もしそれが可能であれば第二種永久機関となってしまう。 そこで考えられたのが、ファインマンズ・ラチェットに対してうまい具合にエネルギーやゆらぎを加えて、ランダムな熱運動を特定の方向に導くといったモデルである。

しかし、現在のところこれらのモデルは発展途上の段階にあり、どこか決定打に欠くように思える。

最大の難点は熱統計力学からの批判であろう。 古典的な熱統計力学の考え方からすれば、そもそも熱ゆらぎというものは「全くの無価値」であって利用することはできない。 途中の経過がどうであれ、最終的に熱ゆらぎから自由エネルギーを稼ぎ出すことはできない、というのが熱統計力学からの要請だ。 当然ながら、既存のモデルは熱統計力学からの要請を考慮に含めている。 基本的にはATPといった形で自由エネルギーを取得し、取得したエネルギーを越えない範囲で出力を行う。 これだと確かに矛盾はないが、ならば、なぜわざわざ熱ゆらぎを介する必要があるのだろうか。 最初に利用可能な自由エネルギーがあったなら、それをいったん間接的に熱ゆらぎに委ね、その後に運動エネルギーに戻すといった方法はひどく迂遠であろう。 既存の熱ゆらぎモデルに明白な矛盾点があったとは言わないが、熱ゆらぎを利用せねばならぬ必然性に乏しい。 「熱ゆらぎの必然性」、これが熱ゆらぎモデルの説得力を損なう最大の問題なのではないか。 逆に言えば、この辺りに生体の持つ謎と魅力が潜んでいる。 熱ゆらぎを利用するメカニズムも必然性も、まだよく解っていない。 それが明らかになれば、これまで人間が作ってきた機械とは全く別の発想に基づく「生体機械」が作り出せるかもしれない。

さて、ここから先は不確定分子モーターの考え方に移る。
　　「出力が不確定でありさえすれば、熱ゆらぎは利用することができる。そして出力に直接寄与することができる。」
不確定分子モーターが掲げたのは、熱統計力学の常識を打ち破ることだ。 打ち破るといっても、熱力学第二法則を打ち破るのではない。 確定的な、決定論的な機械のデザインを打ち破るのである。 不確定な、あいまいなデザイン、それはゆらぎを利用する為の巧妙な仕組みだ。 かつて人が作ったことのない「生体機械」の秘密はここにある。 従来の常識に従って、熱ゆらぎが最終的な出力に寄与しないという制限内で考える限り、いかに小手先のモデルをいじっても本質には達しない。 結局のところ正面から熱力学第二法則という大物に取り組まなければ「生体機械」の本質は見えてこないのである。 熱ゆらぎは、理論上それだけで、他に何の自由エネルギー消費なしで利用できる。 不確定分子モーターの導き出した答は、確かに常識からかけ離れたものに見える。 それは一見すると第二種永久機関のようにも思えるが、出力が不確定であるがゆえにエントロピー増大則に反してはいない。 熱力学第二法則が禁止していたのは「熱ゆらぎの利用」ではなく「熱ゆらぎの確定的な利用」だったのである。

　　「熱ゆらぎは直接出力に寄与することができる。」
ひとたびこの考え方を受け容れてしまえば、筋肉のモデルに新たな視点が開けることになる。 まず熱ゆらぎを利用する必然性について、はっきりした答が用意できる。 熱ゆらぎは、そのまま出力に用いられている。 つまり、出力を増大するために熱ゆらぎを取り入れているのである。 理論上は、最初に用意したATPの持つエネルギーを越える出力を得ることも不可能ではない。 しかし実際には「02 補助動力としての熱ゆらぎ」の節で述べた理由により、熱ゆらぎはATPの補助といった位置づけにある。

不確定分子モーターの要請は「出力が不確定であること」だけだ。 それ以上の具体的な構造について何ら言及するものではない。 タンパク質の分子が折れ曲がるとか、非対称なのこぎりの歯状のポテンシャルが関与しているとか、そういった詳細について明確な予言を与えるわけではない。 しかし「不確定な出力パターン」に本質があると知った以上、構成部品の非対称な形状自体に重要性は無いものと思われる。 非対称なのこぎりの歯状のポテンシャルは、直感に訴えはすれど本質的ではないと私は考える。 次に、のこぎりの歯状ポテンシャルを用いたモデルを検討し、本質的な部分とそうでない部分を選り分けてみよう。

まず検討対象となるモデルを定めよう。 ここでは「日経サイエンス2001/10月号 カオスから生体分子モーターへ」という記事をベースに話を進める。 この記事は必ずしも最新かつ詳細なものではないが、内容が一般向けであって解りやすい。 以下は記事の内容を元に、私なりにまとめた「のこぎりの歯状ポテンシャルモデル」の説明である。

熱ゆらぎにさらされている生体分子を日常の世界で例えるなら、それはちょうど嵐の中で激しく雹がぶつかっている自動車のようなものだ。 自動車は雹がぶつかる勢いで、絶えず前後に揺さぶられている。 この状況下で自動車はエンジンをかけずとも、単にブレーキをかけたり外したりするだけで緩やかな坂を登ることができる。 ここで用いるブレーキには、非対称な歯先を持ったラチェットを想定する。 ブレーキの作り出すポテンシャルはのこぎりの歯のように、一方が急峻で、他方がなだらかな斜面を持つ山を形作っている。 ブレーキをかけた状態で、自動車はのこぎりの歯状のポテンシャルの谷間で止まっている。 ここでブレーキを解除すると、雹の衝突によって自動車は前後にランダムに揺さぶられる。 緩やかな坂道を下るか、一瞬だけ上に登るかは確率の問題となる。 再びブレーキをかけ直すと自動車の位置はどこかのポテンシャルの谷間に収まる。 このときは必ずしも元いた谷間と同じ位置に戻るとは限らない。 ランダムなゆらぎによって、ある確率で１つ先に進んだり、手前に戻ったりするだろう。 問題なのはその確率である。 ポテンシャルの歯先が非対称なため、急峻で短い斜面の側に落ちこむ確率より、なだらかで長い斜面に落ち込む確率の方が高い。 何度もブレーキをかけたり外したりを繰り返すうちに、自動車の位置はより確率の高いなだらかで長い斜面の側に向かって前進することになる。 多少緩やかな上り坂であっても、それ以上にポテンシャルの歯先が非対称であれば、ブレーキの操作だけで自動車は坂を上ることができる。

以上の説明はたとえ話ということもあって、さほど厳密なものではない。 しかし大雑把ではあるにせよ、この説明にはどうも腑に落ちない点が見受けられないだろうか。 一番の問題は「ブレーキを踏むのにエネルギーを要する」という点だ。 そして、日常的な世界の力学をあてはめるなら、ブレーキを踏むのに要するエネルギーの方が、直接自動車を押して坂を上るのに要するエネルギーを上回ることになる。 ここでは２つの角度からモデルを見直すことにする。 １つは力学的な機械と見なす方法。 もう１つは気体分子の圧縮、膨張といった観点から評価する方法である。

まず１つ目の力学的な見地から。 ブレーキを踏み込む、つまりポテンシャルを変化させるには、どの程度のエネルギーが必要となるだろうか。 その答はブレーキの踏み方によって変わってくる。 急激に、一瞬のうちにブレーキを踏んだ場合、ブレーキはポテンシャルの山の高さの分だけ上に乗っているものを持ち上げることになる。 もし対象が山頂の近くにあれば、ほぼポテンシャルの山の高さに相当するエネルギーを要する。 対象が谷底にあれば持ち上げる必要はないので、エネルギーはほとんど要しない。 つまり、ここで要するエネルギーは確率との積分で与えられることになる。 ブレーキを踏んだときに費やしたエネルギーは、ブレーキを解除するときに回収できるかもしれない。 もし踏み込み操作と解除操作が全く逆の関係にあったなら、費やしたエネルギーの回収も可能であったろう。 しかし、このモデルの特性から考えてエネルギーの回収は期待できない。 踏み込み操作と解除操作が非対称な関係にあるからこそ、自動車の前進があり得るからである。 それでは、踏み込み時に費やしたエネルギーはどこに消えるのだろうか。 日常的なマクロな機械であれば、それは熱運動に消えている。 仮に熱運動に消えたとすると、マクロな機械であればそれは無駄な、非効率的なエネルギー消費ということになる。 そうではなく、踏み込んだエネルギーは対象の運動となって保持されるのだとしたらどうか。 この場合、自動車の位置は「谷底に引っかかっている」のではなく、「元の位置と谷底との往復運動」となるはずだ。 そして自動車の位置の滞在時間を考えると、直感に反して低い谷底に位置するよりも山頂近くにある時間の方が長い。 （固い床の上で弾んでいるボールを想像してみよ。最も速いのは床で弾む直前、直後であり、最も遅いのはボールが頂点に位置するときだ。） この滞在時間の分布は、モデル全体にとっていささか都合が悪い。 自動車の位置が谷底ではなく山頂付近にあったのだとすれば、次のステップで坂を上がる確率は低くなるであろう。 結局のところブレーキの踏み込みに要したエネルギーは、無駄になるか、坂を上がる確率を下げるかのいずれかとなるのである。 それでは、ブレーキをゆっくりと徐々に踏み込んだ場合はどうか。 この場合、踏み込みに要するエネルギーは自動車が坂を上がるだけのエネルギーと等しくなる。 要は、単に三角の車止めを用いて自動車を後から押し上げるのと同じことだ。 それならばなぜ、わざわざブレーキの解除を行って自動車を熱ゆらぎにさらす必要があるのだろうか。 坂を上るに際して、三角の車止めをそのまま押し上げれば済む話ではないか。

上ではモデルを力学的な機械と見なしたが、同じことを今度は気体分子の圧縮、膨張といった観点から眺めてみよう。 熱運動している自動車が取り得る位置を狭い範囲に制限するという操作は、熱運動する気体分子を圧縮する操作に等しい。 ブレーキをかけて自動車をポテンシャルの谷間に押し込めるには、大きく分けて２通りの方法がある。 １つは断熱圧縮、もう１つは等温圧縮である。 断熱圧縮は、上の力学的な説明での急激にブレーキを踏んだ場合に相当する。 このとき気体の温度が上昇する。 そして、その上昇した温度は決して特定の方向、例えば「前向き」だけには作用しない。 もしここで自動車を前向きに走らせることを考えるなら、上昇した温度を「冷却して」、自動車の位置をできるだけポテンシャルの谷底近くにもってくることが必要となる。 つまり熱力学の教え通り、ブレーキで「暖め」、何らかの方法で「冷却」すれば、自動車は前進することになる。 これはまさにファインマンズ・ラチェットそのものである。 そして、ファインマンズ・ラチェットにおいて出力に寄与するのは温度差であって、嵐のような雹によるランダムな運動は結果的に何物も寄与しない。 一方、等温圧縮の場合は、上の力学的な説明でゆっくりとブレーキをかけた場合に相当する。 このときは、単純に圧縮操作がそのまま坂を上る操作となっている。 自動車は掛け値なしに、圧縮した分だけ坂を上ることになる。 というより、そもそも圧縮を考えること自体にあまり意味がない。 ここでも雹によるランダムな運動はプラスに作用してはいない。

以上の様に単純な機械と見なした場合、のこぎりの歯状のポテンシャルには有意性が認められない。 それでは、のこぎりの歯状ポテンシャルモデルは１００％間違っているのだろうか。 そうでもない。 熱ゆらぎの利用を前提としたモデルでは、結果として不確定な出力が期待される。 この側面において、モデルと不確定分子モーターの要請は一致している。 不確定な動作を行うといった側面に着目すれば、のこぎりの歯状ポテンシャルモデルは学ぶべき要素を含んでいるのである。 全てが間違っている、あるいは全てが正しい、といった単純な白黒の断定はできない。 上ではブレーキを踏むタイミング、つまりポテンシャル変動の与え方に特別な注意を払わなかったのだが、この点については検討し直す価値がある。 重要なポイントは「規則性」だ。 例えば交流電源は往復運動ではあるが、規則性を持っているが故に電源としての価値がある。 つまり交流電流はエントロピーが小さいのである。 ある程度の規則性を持った脈流であれば、そこに規則性を有している分だけの利用価値がある。 脈流の持つエントロピーを算定し、全エネルギーからエントロピーに対応するだけの分を差し引いた値が利用可能なエネルギーとなる。 ランダムな熱ゆらぎに対してランダムなポテンシャル変動を与えても、そこから有用なエネルギーが取り出せるとは考え難い。 そうではなく、何らかの規則性を持ったポテンシャル変動を与えれば、そこに与えた規則性の分だけのエネルギーが取り出せる可能性がある。 不確定分子モーターの考え方では、出力が不確定であれば、その分だけ利用可能なエネルギーが稼ぎ出せる出せるということであった。 これらの規則性、不確定、エントロピー（この３つは同じことを言っているのだが）を総合すると、

といった図式が成り立つ。 重要なのは「規則的かランダムか、決定的か不確定か、エントロピーを含むか否か」なのだ。 それに比してポテンシャルが非対称であることは、実のところ副次的な意味合いしか持たない。※ 私としては、のこぎりの歯状のポテンシャルのことはいっそ忘れた方が良い様に思う。 ポテンシャルの変動はむしろ単純にＯＮ，ＯＦＦのスイッチング素子として捉える。 そして、ＡＴＰ由来の信号が常にゆらぎの観測を行っており、チャンスが来た瞬間にスイッチをＯＮにする。 これが先の章で述べた「悪魔の装置」のメカニズムであり、おそらく熱ゆらぎを積極的に利用する機械全般にあてはまる。 いたずらに確率微分方程式やコンピューターシミュレーションに挑む前に、情報の流れについて原理的な考察が不可欠であろうと思うのである。