ブラウン運動モーターの Java Applet が
このページ にありました[英語]。
このページは、Applet の解説を日本語訳したものです。
あと、このページに解説があります。
気になる科学探検隊「マクロスケールの常識を覆す分子モーター」
In his famous lectures Richard Feynman discussed the impossibility to violate the second law of thermodynamics by a ratchet mechanism.
リチャード・ファインマンは彼の有名な講義の中で、ラチェットメカニズムを用いて熱力学第二法則が決して破れないことを語った。
The simplest model for a ratchet is an overdamped Brownian particle in an asymmetric but spatially periodic potential
(with asymmetry α and period L).
もっとも簡単なラチェットのモデルは、ブラウン運動粒子を非対称な、空間的な周期性を持ったポテンシャル中に置いたものだ
(非対称性α、周期L)。
Due to the fluctuating force caused by the pushing molecules of the surrounding fluid or gas the Brownian particle may overcome the potential barrier moving to the left or to the right.
周囲にある流体か気体が分子を押すことによって引き起こされる揺らぎの力のため、ブラウン粒子はポテンシャル障壁を左か右に動いて乗り越えるだろう。
The probabilities for both directions are equal.
(右左)両方向の確率は等しい。
Thus on average the particle does not move.
かくして平均すると、粒子は(左右どちらか一方には)動かない。
Hence building a motor which turns thermal energy into mechanical work from a single heat bath is impossible.
それゆえ、単一の熱浴からの熱エネルギーを機械的な仕事に変えるようなモーターを作成することは不可能なのだ。
But the ratchet can be turned into a so-called a Brownian motor that seems to violate the second law of thermodynamics.
しかし、ラチェットは、いわゆるブラウン運動モーターと呼ばれているものに作り変えることができる。
そしてそれはあたかも熱力学第二法則を破っているかのように見える。
The idea is to turn the ratchet potential periodically on and off with a frequency 1/2τ.
そのアイデアとは、ラチェットポテンシャルを周期的に、周波数 1/2τ でON/OFFすることだ。
Under certain circumstances this may yield directed motion even against an applied force f.
この状況下だと、一方向の運動を得ることができる。しかも、逆方向の力fを与えてさえも。
It is indeed a device doing work.
これは本当に動くものなのだ。
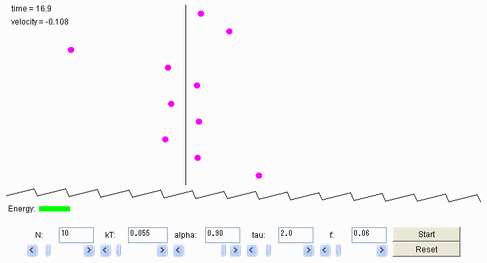
Below you can play with a Java applet which simulates such a system.
以下で、このシステムをシミュレートした Javaアプレットを動かすことができる。
Vary the parameters and figure out the condition for a drift from right to left even for f > 0.
パラメーターをいろいろ変えてみて、たとえ力f > 0 がかかっていても、右に動くような条件を探してみよう。
If you want to know why a Brownian motor isn't a perpetuum mobile of the second kind click on "here".
なぜブラウン運動モーターが第二種永久機関でないのか知りたい人は、下の説明を見よ。
* Parameters can be changed either by manuipulating the corresponding scroll bar or by directly putting a number into the number field.
パラメーターはそれぞれスクロールバーか、直接数値を入力することによって変えることができる。
There are the following parameters:
次のようなパラメーターがある:
N = 粒子の数.
kT = thermal energy kT in units of the potential barrier.
kT = ポテンシャル障壁のユニット内の熱エネルギー kT (k:ボルツマン定数、T:温度)
alpha = asymmetry α of the ratchet potential.
alpha = ラチェットの非対称の度合いを表す数値 α.
tau = switching time τ.
tau = スイッチ切替時間 τ.
f = applied force f in units of the potential barrier divided by L.
f = ポテンシャル障壁のユニット内に働く外力f、Lで割ったもの。
* The start/stop button starts or stops the animation in the animation area.
start/stop ボタンは、アニメーションを開始、または停止する。
* The reset button resets the particle positions.
resetボタンは、粒子の位置を初めの状態に戻す。
* The animation area shows:
アニメーションエリアの表示は:
1. The result of the simulation. シミュレーション結果
粒子の数が20以下の場合、粒子は円形で示される。
For a larger ensemble the particle positions are shown as a function of time (time direction is pointing upwards).
(21個以上になると)多数の粒子集団の位置が時間の関数として示される(時間経過は上方向に進む)。
The black line shows the averaged particle position.
黒い線は粒子の位置の平均を表す。
In the upper left corner the time and the averaged velocity (assuming L = 1) are shown.
左上の隅に、時刻と平均速度(L = 1 として)が示してある。
有効なポテンシャルは黒で示される。
When the saw-toothed part is switch off it is still shown in light gray.
のこぎりの歯のような部分はスイッチOFFのとき、灰色になる。
The potential is tilted due to the external force f.
ポテンシャルは、外力fがかかると斜めに傾く。
ポテンシャル・エネルギーの平均を緑色の棒グラフで示した。
なぜブラウン運動モーターは第二種永久機関にならないのか?
As long as the ratchet potential is off the particle will move diffusively according to a (biased) random walk,
ラチェットポテンシャルがOFFになっている間、粒子は(バイアスのかかった)ランダムウォークのため拡散的に動くだろう、
leading to a variance in position of Δx = √2Dγ and a mean position of <x> = fτ/γ,
位置の分散 Δx = √2Dγ と、位置の平均 <x> = fτ/γ から導かれるように。
where D = kT / γ is the diffusion constant.
ここで D = kT / γ は拡散定数を表している。
When the ratchet potential is switched on, the particle gets trapped in one of the potential minima.
ラチェットポテンシャルのスイッチがONになったとき、粒子はどこか1つのポテンシャルの谷に捕らえられる。
If αL >= Δx >= (1-α)L for the variance holds, the particle on average gets trapped into the minimum left to the starting point.
もし分散を αL >= Δx >= (1-α)L というように保てば、粒子は平均してスタート地点より右側の最小値に捕らえられるだろう。
The maximum flux is obtained if the switching time τ is large enough to assure that the particle can adjust in the trapping minimum ('adiabatic adjustment time') and also is small enough to fulfill the above requirement for the variance.
スイッチ切替時間τが、粒子が谷底にはまるまで補正できる時間(断熱補正時間)よりも確実に十分大きく、かつ上の分散についての要求を満たすよりも十分小さかった場合に、最大の流れが得られる。
One can say roughly that a net flux to the left always occurs, when thermal energy is significantly smaller than the potential maximum,
大雑把に言えば、左側の流れは常に生じているが、熱エネルギーはポテンシャルの谷よりも十分小さい、
the external force is chosen not too big and the driving frequency matches the adiabatic adjustment time needed for the particle to move into a potential minima.
なので外力がそれほど大きくならない一方で、原動力の振動は粒子がポテンシャルの谷底まで動くのに必要とされる断熱補正時間にちょうど合っている。
Where does the energy come from leading to a drift against the external force?
外力に逆らうエネルギーはどこから来るのだろうか。
The energy does not come from the heat bath but from the ratchet potential when it is switched on.
エネルギーは熱浴から来るのではなく、ラチェットポテンシャルがスイッチONになるときに得られる。
At that moment the potential energy of the particle will be suddenly increased.
スイッチが入った瞬間に、粒子のポテンシャルエネルギーは急激に増加する。
In the simulation this can be seen by a sudden increase of the energy bar.
シミュレーションでは、エネルギーの棒グラフの急増が見てとれる。
But most of the energy pushed into the system will be just dissipated into the heat bath
しかし、システムに入れ込んだエネルギーの大半は熱浴に消えている、
due to the relaxation of the particle into a potential minima.
粒子がポテンシャルの谷間へと緩和されるときに。
Only a tiny portion will be used for doing work.
ごく一部(のエネルギー)だけが、働くのである。
Thus a Brownian motor does not violate any law of thermodynamics it only turns one type of work into another one.
かくして、ブラウン運動モーターは熱力学第二法則を破ってはおらず、単にある種の仕事を別の仕事に変えているだけだ。
Nevertheless the fluctuating force due to the heat bath is essential for a Brownian motor.
決して熱浴からの揺らぎの力がブラウン運動モーターにとって必須なのではない。
For more details and possible applications in biology and chemistry read the following review article:
もっと詳しい生物学や化学への応用は、次の記事を参照のこと:
R.D. Astumian: Thermodynamics and Kinetics of a Brownian Motor, Science 276, p. 917-922 (1997).