参考リンクに挙げた、 学習院大 田崎先生のサイト 上に興味深い問題が載っていました。 以下に引用します。
一昨日の晩につくってしまった(12/14)第二種永久機関をここだけで公開!
質量 m の質点 N 個が集まってできた物体を考える。 質点の間には、任意の力(通常どおり全体の並進について不変)が働いていて、この物体をひとまとめにしている。 簡単のため、1次元系を考察するが、3次元への拡張は自明。
はじめ、物体の重心は、速度 V で x 正方向に動いている。物体の内部自由度は、温度 T の平衡状態にある。 よって、各々の質点の速度は、この重心の速度 V に、熱運動によるゆらぎを付加した V + v である。 V は共通だが、v は質点ごとに異なる。ただし、|v| は V に比べてずっと小さいとする。
この物体が、ポテンシャル 0 の x < 0 の領域から、ポテンシャルの低い x > 0 の領域に入り、加速する状況を考える。 各々の質点の感じるポテンシャルは、x < 0 では 0 であり、 x > 0 では - m u であるとする。 ここで x は座標であり、u は正の定数。
もし、内部自由度のことを考えなければ、原点を通過すると、物体のポテンシャルエネルギーは M u だけ下がる(M = m N は物体の全質量)。 よって、原点を通過したあとの物体の速度 V' は、エネルギー保存則
(M/2) V^2 + M u = (M/2) (V')^2
により決まる。(V^2 というのは、V の二乗のこと。)よって
V' = ( V^2 + 2 u )^(1/2)
となる。
ここで、V が非常に大きいと仮定する。 よって、物体は、ポテンシャルが急激に変化する x = 0 という場所をきわめて短時間で通過する。 時間が短ければ、質点の間に働く力の効果は小さくなる。 以下では、物体が原点を通過している間の質点間の相互作用を無視する。 (よって以下の結果には、質点間の相互作用による補正がつくはずだが、それは、V を大きくすればいくらでも小さくなる。)
初速度 V + v を持っていた質点が、原点を通過した後の速度 V'' は、やはりエネルギー保存則
(m/2) (V+v)^2 + m u = (m/2) (V'')^2
より
V'' = ( (V+v)^2 + 2 u )^(1/2)
と求められる。無論、v = 0 とすれば、これは上の V'' に一致する。 v が V よりはるかに小さいと仮定したので、この表式を v について二次まで Taylor 展開しておこう。
V'' = V' + { V (V^2 + 2u)^(-1/2) } v + { 2 u (V^2 + 2u)^(-3/2) } v^2 + O(v^3)
これが、N 個の質点各々について成り立つ。 原点を通過したあとの重心の速度 Vfinal は、この V'' を N 個の質点すべてについて平均すれば、求まる。 v は熱運動によってばらついているので、明らかに、v の平均は 0。 他方、(m/2)v^2 の平均が (kT/2) 程度であるべしということから、 v^2 の平均は (kT/m)^(1/2) 程度と知れる。よって、
Vfinal = V' + 2 u (V^2 + 2u)^(-3/2) (kT/m)^(1/2) + O(v^3)
となり、最終的な重心の速度は、内部自由度を無視した場合の V' より真に大きい。 (kT/m) = (NkT/M) であるから、これは別に微小な量ではないことを強調しておく。
もちろん、(磁力発電とは違って)エネルギー保存は成り立っているので、重心の速度の増加分は内部運動のエネルギーから来ている。 (実際、T=0 では Vfinal = V' であって、内部自由度を無視した力学の答がでる。) つまり、ポテンシャルの境目(原点)を通過する際に、内部自由度の熱エネルギーの一部が重心の運動の力学的エネルギーに転換された ことになる。(これはエネルギー保存則に反しない。この系には運動量保存則は、もちろん、ない。)
ところが、ここでは、熱力学第二法則で禁止されている熱エネルギーの力学的エネルギーへの直接の変換がおこなわれている。
つまり、これが正しいと、第二種永久機関ができる。
よりサイクルっぽくしたければ、右図のようなポテンシャルをつくり、周期的境界条件にしておくとよい。
はじめ、物体をある温度にしておき、重心にはポテンシャルの山を越えられる程度の右向きの速度を与えておく。
すると、山を越えるときに、上の機構が働き、物体は力学で予想される以上に加速され物体の温度が下がる。
(ポテンシャルが不連続に変化するところ以外では、質点には一様な力が働くので、重心運動と内部運動は完全に分離する。
重心は力学どおりの運動をし、内部自由度は新たな熱平衡に緩和するだろう。)
よって、一周して出発点に戻るときには、はじめに同じ点を通過したときよりも大きな速度をもつことになる。
これをくり返すことで、物体の温度が下がりきるまでは、物体は加速をつづける。
サイクロトロンのようだが、静的なポテンシャルによる連続した加速であることに注意。
物体が適度に加速し、温度が下がったところで、運動エネルギーを何らかの方法で回収する。 これは、最初に物体に速度を与えるのに必要なエネルギーより真に大きいから、エネルギー収支はプラスである。 そのため物体の温度は下がっているが、物体を空気等の環境に接触させれば、その温度を再び上げることができる。 これを繰り返せば、単一の温度の環境から熱を吸収して繰り返し仕事に変換することができる。21世紀のエネルギー問題は解決する。
同じ話で、u を負にとると、V'' における v^2 の項の係数は負になり、この場合は、内部自由度へのエネルギーの散逸による減速というまともな話になる。面白いことだが、u が正の上の話が冗談であるにもかかわらず、こちらの散逸の話は、ある種のモデルで厳密化できる可能性がある。
こんなサイトを作っておいて言うのもなんだが、こと永久機関のうそを見破ることについては、私は少々うるさい。 これまで事あるごとにあちこちの永久機関を漁っては調べてきたが、 その中にあって、この「ドクター田崎エンジン」は、おそらく最強の一品ではないかと思う。
一見して、どこにうそがあるのか全く分からず、かなり考え込んだ。
・・・まさか・・・
しかし、世の中そんなに上手い話は転がっていない。考えた末、こんな答にたどりついた。
この問題のヒントは「二人三脚」にある。 二人三脚とは、運動会で2人の足の片方ずつをはちまきで縛って走る、あの競技のことである。 もし2人の歩調がぴったり一致していれば、二人三脚の速さは1人で走った場合と変わらないはずだろう。 しかし、実際には歩調が一致せず、必ず一方が他方の足を引っ張ってしまう。
これと似たような話が、熱振動する分子についても言える。 もし分子が1個だけだったなら、問題の説明通り、ポテンシャルの落下地点で{振動エネルギー → 並進運動エネルギー}の変換が行われるだろう。
それでは、2個の分子が「二人三脚」のようにつながったまま、ポテンシャルの落下を行ったならどうなるか。 もし2個の分子の「足並み」がぴったりとそろっていれば、つまり、振動の位相がぴったり一致していれば、1分子と同じように{振動 → 並進}の変換が行われる。 しかし、もし足並みがそろっていなかったなら、つまり、振動の位相がずれていたならば、2個の分子の加速が異なるため、一方が他方の足を引っ張ることになる。 振動の位相がずれていたなら、振動エネルギーは必ずしも全て並進運動に転じるわけではない。 同時に、一方の振動子から、他方の振動子へのエネルギー移動も起こる。 なので、振動エネルギーが一方的に減少し、並進運動が一方的に増大するということにはならない。
さらに分子数を増やして、二人三脚ではなく、三人四脚、五人六脚、、、と増やしていったらどうなるか。
実際に1クラス10数人ほどの人数で競争しているのを見たことがある。
この人数になると、いかに足並みをそろえるかが重要になってくる。
お互いに声をかけあって「イチ、ニ、イチ、ニ」で歩を運ばないと、前進することすらままならない。
同じことが分子でも起こる。
位相のそろっていない多数の分子がポテンシャルの落下を行えば、エネルギーの大半はお互いの振動間のやりとりに費やされてしまい、ほとんど並進に回ってこない。
なので、多数の分子から成る物体の熱振動が「そろいもそろって」並進エネルギーに転ずることはほとんどあり得ないのである。
ここで、もし全ての分子の「足並みがそろっていたら」、つまり振動の位相が一致していたらどうなるか。 その場合には、例外的にポテンシャルの落下によって振動エネルギーを並進エネルギーに変換することができる。 足並みがそろっていた場合に限り、エネルギーの取り出しが可能なのである。
それではもし仮に、多数の分子の「足を縛ることなしに」互いに独立したまま、ポテンシャルの落下を行ったらどうなるか。 この場合には「足の速い分子と遅い分子」が出ることになる。 つまり、分子が拡散する。 拡散した分子を1つに集めようとすれば、それは熱運動する気体分子を圧縮することになるから、自由エネルギーの消費が避けられない。 なので、個々の分子をばらばらに落下させることによって、並進エネルギーを取り出すことはできない。
この問題のポイントは「多数の分子の」「位相がバラバラなこと」にある。 1個の分子だけを扱う限りにおいては、矛盾は見えてこないし、事実、矛盾はない。 例えばレーザー光線は、波長と位相がぴったり一致した光のことである。 位相が一致している状態は、ばらばらな状態よりも「利用価値が高い」。 すなわちエントロピーが小さい。 てんでんバラバラに運動する「利用価値の低い」分子集団から、利用可能な並進エネルギーを取り出すことはできないのである。
直感的なたとえ話ではなく、まともな計算で答を示すのは、かなり難しい。
そこで、計算の代わりにパソコン上のシミュレーションで動作を確かめてみた。
(シミュレーションの動作に必要なソフトはこちらを参照のこと。)
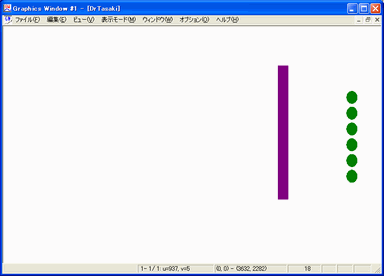
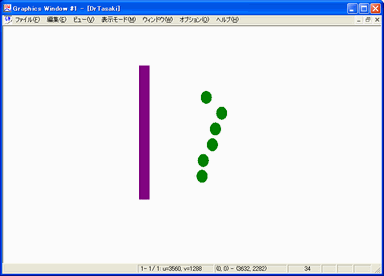
なので、振動エネルギーが一方的に並進運動エネルギーに変換されないことが確認できた。

