コンピュータが演算を行う過程で生じるデータのゴミ処理には、エネルギーの消費が避けられない。 この考えを応用すれば、なぜ第二種永久機関が実現できないかについての明確な説明を与えることができる。 マックスウェルの悪魔のパラドックスに対する解答は、コンピュータのエネルギー消費についての考察から得られたのである。 このことを最初にはっきりと述べたのは、Ｃ．ベネットという人物である。 ベネットの考察については第一章でも簡単に触れたが、ここでいま一度、その内容について再確認しよう。

コンピュータと第二種永久機関、一見すると何の関係も無い取り合わせに思えるかもしれない。 しかし、実のところ両者は同一物の表と裏の姿なのだ。 物理法則の許す範囲内で情報処理を行うのがコンピュータ、物理法則を越えて情報処理を行うのが第二種永久機関である。 なのでコンピュータの物理的限界がどこにあるのかを突き止めれば、第二種永久機関が不可能なことは自ずと明らかになる。 それでは、ここで言う物理法則、物理的限界とはどのようなものだろうか。 一言で言えば、それは「エネルギーの損失なしに２状態を１状態にすることはできない」ということだ。

ビリヤードボールコンピュータの動作を思い起こしてみよう。 各々のボールが定められた軌道の上を転がっている間は、エネルギーの損失は無い。 問題は演算を終えた後、行き先が分からなくなったボールを回収する過程にある。 ボールを回収するには、ボールがたどり着く可能性のある全ての場所をチェックしなければならない。 全ての場所に箱を置いてボールを回収したとしても、ボールの入った箱と空の箱とを１つにまとめる段階でエネルギーを要する。 これは前節に述べた通りである。 箱という仕掛けを用いず直接的に、全てのボールの軌道を共通の「回収ポイント」に向わせれば良いと思われるかもしれない。 しかし、異なる複数本の軌道を１本にまとめ上げる段階で、やはりエネルギー消費が避けられない。 これは第２章で考えた「合流タイプ」に相当する。 つまり、箱であれ、メモリーであれ、軌道であれ、「どちらにあるか分からない複数の状態」を「１つの状態」に戻すには、相応のエネルギーを必要とするのである。

ところで、「行き先が分からなくなったボール」というのは「行き先が分からなくなった分子」と一脈通じる節がある。 例えばエンジン（熱機関）は、小さく圧縮された気体が膨張する過程を通じて仕事を取り出している。 小さく圧縮された気体は大きく膨張した気体に比べて、分子の位置をより狭い範囲に特定できる。 言い換えれば、大きく膨張した気体の分子はより「行き先が分からなく」なっている。 ひとたび大きく膨張した気体を元の小さく圧縮された気体に戻すには、力を加えて押し込めるなどの操作が必要となる。 どこにあるかわからない、より広範囲に散らばった対象を、はっきりと一カ所に、あるいは限定的な範囲に押し戻すには、相応のエネルギーを必要とする。 コンピュータのボールと気体分子は、こういった共通の原理に従っていたのだ。 気体分子の取り得る範囲の広さのことをエントロピーと呼んでいた。（より正確には範囲の広さの対数） コンピュータのボールは気体分子の様に連続的な範囲を取らない。 （量子的に考えれば気体分子も必ずしも連続的ではないのだが。） また、コンピュータの取り得る状態数は膨大な数の気体分子とはオーダーが異なる。 確かにそういった違いはあるのだが、エネルギーの挙動から考えるとコンピュータの取り得る状態数をエントロピーと呼んでも良いのではないか。 いずれにせよ、コンピュータと熱機関は原理的に同じメカニズムによってエネルギーを消費している。 その原理を直感的に言えば「ばらばらに散らばったものを元通りに集めてくるのにエネルギーを要する」ということなのである。

ベネットの考察が革新的であったのは、コンピュータの原理が熱機関にもあてはまることを指摘した点にある。 ここでいま一度、第１章”シラードの悪魔”を振り返って、ベネットの主旨を追ってみよう。 シラードの悪魔とは次の様なものであった。 熱運動から有用な仕事を取り出すためには、ばらばらに散らばった分子を何らかの手段を用いて一カ所に（あるいは特定の狭い領域に）集めて来なければならない。 端的な場合として、部屋の中にただ一個だけの分子が運動している状況を想定しよう。 ある瞬間に部屋の中央に仕切を入れれば、分子は部屋の右半分か左半分かの狭い領域に閉じ込められる。 分子は狭い場所に閉じ込められられたのだから、原理的にはこの状態から有用な仕事を取り出すことができるはずだ。 ただし、分子が右にあるか左にあるかを言い当てることができればの話だが。 ここで、分子が右にあった場合は操作Ｒを、左にあった場合は操作Ｌを実行する装置というものを考える。 この装置は、まず最初に分子の左右を見定める観測の過程と、左右２つの観測結果に対応する操作実行の過程、操作Ｒ実行部と操作Ｌ実行部から成り立つであろう。 操作Ｒ＝「右側にある分子から仕事を取り出す操作」、操作Ｌ＝「右側にある分子から仕事を取り出す操作」とすれば、いずれの場合でも熱運動から仕事を取り出せることになる。 このような装置を組み立てるのは物理的に不可能ではない。（第一章のベネットの装置の図を参照のこと） 問題は操作を終えた後の状態にある。 以下にＬとＲ、両方の操作を表した図を挙げる。

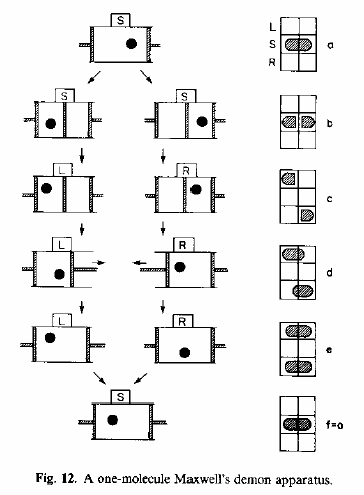
図の右隣に描かれているのは、分子の位相空間を模式的に表したもの、いわば「悪魔の心の中」を描いたものである。 位相空間上の領域の広さは、分子から仕事を取り出す段階で２倍に膨れあがる。 つまり、この段階で分子のエントロピーは増大する。 仕事を取り出し終えた後も、エントロピーは増大したままである。 とことが、ここから次のサイクルの最初の状態に戻ろうとすると、領域の広さは半分に縮むことになる。 つまりエントロピーは減少したことになる。 ということは、仕事を取り出し終えた後の状態から、次のサイクルの最初の状態に移行するまでの間に何らかの矛盾がある。 装置全体のことを考えると、操作Ｒを終えた後の装置は状態Ｒであり、操作Ｌを終えた後の装置は状態Ｌとなっているはずだ。 ここで、状態Ｒと状態Ｌが具体的に何であるかを追求する必要はない。 装置に仕組まれたメモリーの値がＲのときに１で、Ｌのときに０であるとか、あるいは装置内を転がっているボールが軌道Ｒの上を走っているか、軌道Ｌの上を走っているとか、何であっても構わない。 とにかくＲとＬが異なる状態であれば、どこかに異なる２状態を１状態に戻す過程が不可欠となる。 かくして悪魔の装置は物理的な限界に突き当たる。 改めて繰り返すが、物理的な限界とは
　　「エネルギーの損失なしに２状態を１状態にすることはできない」
ということである。 エネルギーの損失とは何であるかというと「明確に運動量が特定できるエネルギーを、運動量がわからない、ばらばらな状態にもってゆく」ことだ。 つまりこの物理的限界は次の様にも言い換えられる。 「何物かを２状態から１状態にしたならば、その代わりに別の何物かを１状態から２状態にしなければならない。」 このとき「２」という状態数を、ある物から別の物に移行するのに必ず一定以上のエネルギーを要するのである。 全体として見た場合、「２」という状態数は最初から最後まで変わることはない。 少なくとも、状態数が自然に減ることはあり得ない。

エネルギー消費の観点から見たとき、コンピュータと熱機関には共通する物理法則が働いている。 それはエントロピーの法則、状態数はけっして減ることはないという法則だったのである。