前節で、エネルギーの最も自然な分布は、ボルツマン分布

に従うということを述べた。 なぜエネルギーの分布はこのような指数関数となるのだろうか。

まず、問題を確認しよう。
「多数の分子にエネルギーを配るときに、最も確率が高くなるのはどのように配分したときか」

最初に、問題をうんと単純化して分子が２個の場合を考える。 分配すべき全エネルギーをＥとしよう。 このとき、１個の分子の持つエネルギーがE1となる確率をPr(E1)とすれば

となるであろう。 なぜなら、分子の持つエネルギーは０〜Ｅの間で均一だからである。

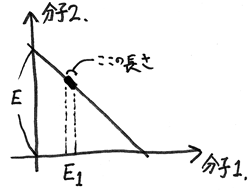
次に、分子が３個あった場合を考える。 ３つの分子の持つエネルギーを E1, E2, E3 として、この３つをそれぞれX,Y,Z軸にあてはめた（立体の）グラフを書いてみよう。 全エネルギー一定という条件は、グラフ上の正三角形の面として表現されている。 E1の軸に着目して三角形を見ると、E1がＥに近づくほど、それに比例して三角形の切り口の長さが短くなる、つまり確率が下がることがわかる。 三角形をE1軸に投影した面積（三角形の切り口の長さの積分）は E^2 / 2 であることを考慮すると、求める確率は

となる。

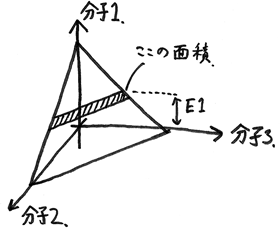
分子が４個になると、図示するのは難しい。（４次元なので） 上の分子３個で用いた様な図を、４個目の分子が持つエネルギーの大きさ順に並べて想像するしかない。 ここでは、着目する分子のエネルギーE1の順に図が並んでいるものと考える。 全エネルギー一定という条件は、今度は個々の図の正三角形を重ね合わせた三角錐の体積として表現されている。 エネルギーがE1であるような切り口の図に着目すると、E1がＥに近づくほど、三角形の面積が小さくなる。 面積は長さの２乗に比例するので、確率は (Ｅ - E1) ^ 2 に比例して小さくなる。 三角錐の体積は E^3 / 3 となるので、求める確率は

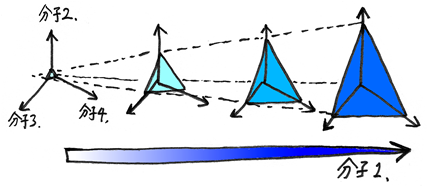
ここまで来ると、分子がもっと増えたときの確率の予想が付くだろう。 分子がｎ+1個あった場合の確率は

となる。
（直線の長さ -> 三角形の面積 -> 三角錐の体積 -> ４次元三角錐の体積(?) -> ... は、Ｎ次の積分を考えればよい） ここで、分子数が非常に大きくなったとき lim(n→∞) を考える。 自然対数 e の定義から考えると ※ ここで全エネルギーを分子数で割った平均値、E/n を A と置くと、 これを用いて 結果はエネルギーE1 に対する指数関数となっていることが確認された。

以上が指数分布の理由なのだが、それでも実感が湧かないという方のために数式抜きの説明を付け足そう。 例えば人生をハードル越えの連続と見なして、生まれ落ちたときには全員が等しくスタート地点に並んでいるものだとしよう。 仮にスタート地点に１万人が並んでいたとする。 １つ目のハードルを越えるときに、そのうちの半数が脱落するものとしよう。 無事ハードルを越えた人数は5000人である。 ２個目のハードルを越えるときにも、残りの半数が脱落するものとする。 すると、２個目を越えた人数は2500人となる。 ３個目で1250人、４個目で625人、５個目で312（又は313人、割り切れないので）、以下半分の人数、半分の人数が残ることになる。 この様子を天から眺めれば、１つ目のハードルに残っている人数が最も多く、ハードルの数が増すにつれて徐々に人数が減っていく分布が見えることになる。 これがまさしく指数分布である。 ハードルの高さは、いわばエネルギーの段差に相当する。 人生のたとえを借りるなら、ハードル一段の違いは持てる財産の違いのようなものである。 （何とも切ない話ではあるが。） 上の例では１つのハードルで半数が脱落するものとしたが、ここで脱落者の割合を80%、90%といった具合に低く抑え、その代わりハードルの数をたくさんに増やす。 その極限として、スタート地点の人数が最も多く、スタートから離れるに従って人数が漸次減少するような分布となるのである。