先の「悪魔の装置」に示したカラクリ、あるいは計算機実験編にある「ワープゾーン」はいかにも技巧的で、 １００歩譲ったところで現実に制作できるとは思えない。
ところが、この複雑な装置を一気に単純化できる（かもしれない）アイデアがある。
それは、ピストンを古典的な板ではなく、量子論的な粒子とする方法だ。

☆以下のアイデアはまったくの荒削り。きちんと見直す必要あり。

「悪魔の装置」で実現が難しいのは、ピストンを箱の端から中央付近まで瞬時に移動することだ。
確かに古典的な物体であれば「瞬間移動」は難しい。
しかし量子論的な粒子であれば、この芸当をやってのけるかもしれない。

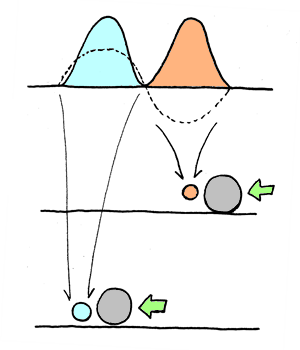
左図のように、確率の山が２つに分かれている波動関数を想定する。
実際に観測が為されるまで、粒子は左右どちらの山にあるのか分からない。
観測、すなわち他の粒子が衝突して初めて、粒子の位置が明らかになる。
この性質をうまく利用すれば、粒子が左右の山の間を瞬時に移動したかのように見える状況を作り出すことができる。

量子論的な「ピストン粒子」は、自然な状態で確率の山が２つに分かれている分布を持つものとする。
このピストンに別の粒子、ここでは熱運動する気体分子が近づくと、ピストンは５０％の確率で１つめの山で、 残る５０％の確率で２つ目の山で衝突することになる。
もし１つめの山で衝突が起こった場合、熱運動する気体分子はピストンを２つめの山の位置まで押して仕事を為す。
気体分子がピストンから離れたなら、ピストンは再び２つの山を持つ確率分布に従う。
次に衝突するときは、ピストンが１つめの山にあるのか、２つめの山にあるのか全くわからない。
これはつまり、ピストンが「半分だけ」瞬時に移動したのと同じことではないか。

つまり、ピストンの移動には、

の２つの経路が存在する。

もちろん、この２つの経路はいずれも可逆である。
なので、経路が２種類あるという理由だけで１→２→１→２･･･ といった一方向の流れが生ずるわけではない。
ここで提示したかったのは、量子論を応用すれば技巧的なカラクリを想定せずとも「悪魔の装置」が構成できる、 ということだ。

例えば「量子ラチェット」といった仕組みを考えたとき、波束の収束による「瞬間移動」は一考に値するのではなかろうか。